Proviamo ad analizzare l’equazione di emissione da pozza presente nella terza edizione della Norma EN IEC 60079-10-1:2021. Come si vede, la portata risulta direttamente proporzionale alla velocità dell’aria che lambisce il pelo libero del fluido (elevata alla 0,78), all’area della pozza, alla tensione di vapore della sostanza infiammabile, alla massa molare (alla 2/3) ed inversamente proporzionale alla costante universale dei gas e alla temperatura assoluta (km è il coefficiente di trasporto di materia, dimensionalmente espresso in [cm/s] o [m/s]. Scopriremo più avanti che è questo un parametro particolarmente importante).
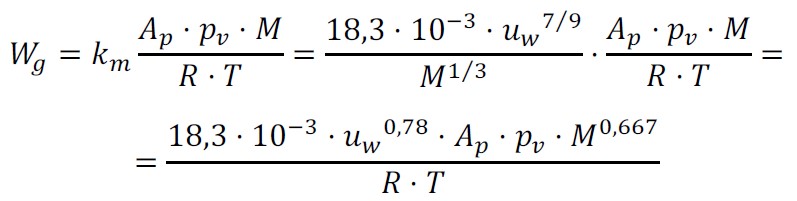
Tuttavia, approfondendo il tema, ci accorgiamo che quella indicata dalla norma è solo una delle molte espressioni empiriche, proposte nel corso degli anni, che hanno cercato di inquadrare la complessità del fenomeno. Una bella sintesi è riportata in Penelon et al, 2020 (cfr. tabella seguente).
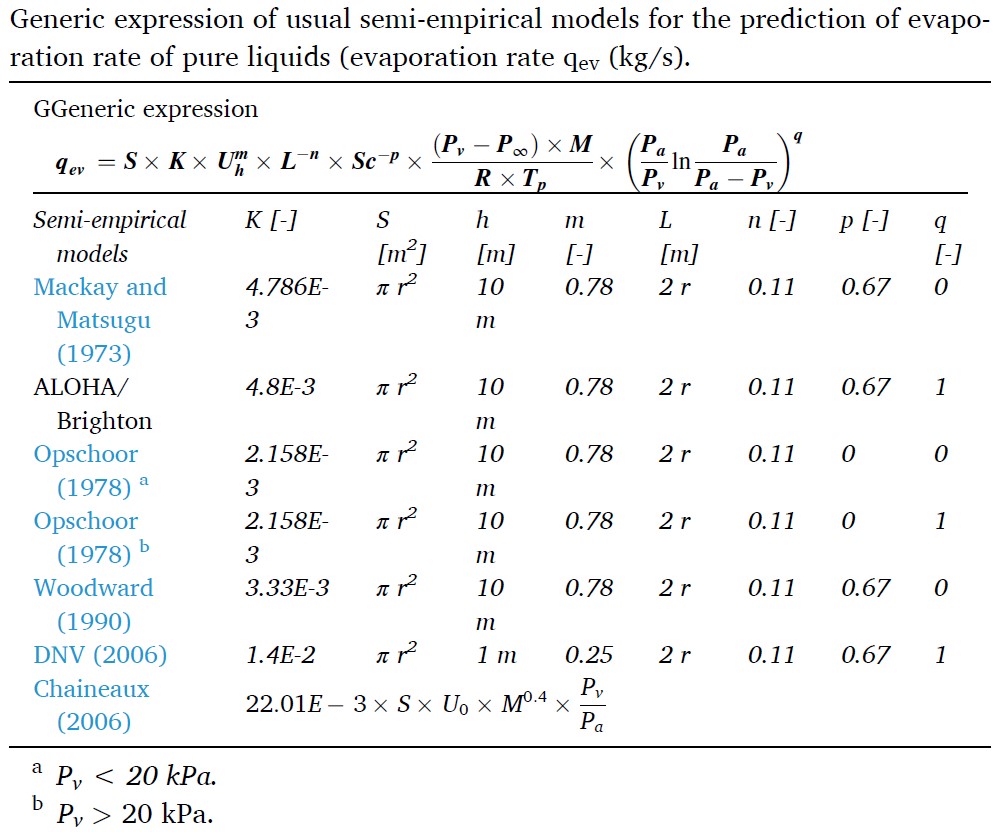
Come qualcuno già saprà, l’equazione sopra riportata, presente nella terza edizione della Norma, differisce rispetto a quella di seguito illustrata e contenuta nella seconda edizione dello standard normativo.
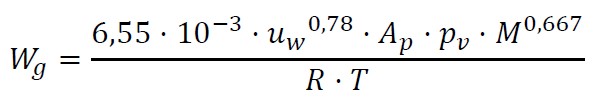
È ora facile constatare che, nella III ed, la portata d’emissione di una pozza di infiammabili è circa 2,8 volte superiore a quella della II ed. Questa modifica è conseguente al fatto che, nella versione EN del 2016, il normatore ha fatto riferimento ad un documento EPA[1] del 1987 mentre in quella del 2021 è presente un’equazione derivata da una successiva pubblicazione dell’EPA del 1999. E, nel report più recente, l’EPA giustifica la modifica/aumento della portata nel modo di seguito riassunto.
- Primo fatto. L’equazione presente nel report EPA del 1987 si basa su un famoso studio del 1973 di Mackay & Matsugu[2] stra-iper-super-citato; un “Avenger” delle pubblicazioni specialistiche poiché sono ben 462 i paper scientifici fondati sulle sue conclusioni. Insomma, vista la numerosità delle “teste pensanti” che l’hanno verificata, possiamo essere confidenti che l’equazione utilizzata dall’EPA rappresenti lo stato dell’arte scientifico sull’argomento.
- Secondo fatto. Il coefficiente di trasporto di materia, il km che ho indicato nell’equazione base, è di norma connesso al coefficiente di trasporto dell’acqua, riproporzionato rispetto alla massa molare della sostanza infiammabile (il motivo di questa correlazione è un po’ lungo da spiegare. Per chi voglia saperne di più c’è il Workshop ATEX 2024).
- Terzo fatto. Nel 1987 è stato assunto in sede EPA un km dell’acqua pari 0,24 cm/s mentre il coefficiente di trasporto di materia adottato nel 1999 è stato di 0,67 cm/s. E 0,67 diviso 0,24 fa proprio 2,8 che è l’aumento riportato nella terza edizione della Norma tecnica.
Ci siamo quindi? L’errore che in questo momento mette in crisi molti tra noi arriva da lontano. Probabilmente è stato causato da un funzionario pubblico statunitense un po’ pasticcione che ha indicato un coefficiente di trasporto di materia dell’acqua irrealistico.
Questione finita?
Non proprio, diciamo.
Se guardiamo alla più recente letteratura specialistica si scopre che il km da adottarsi per l’acqua è di 0,83 cm/s (cfr. Crowl & Louvar, 2019[3]):
“(…) Water is most frequently used as a reference substance; it has a mass transfer coefficient of 0,83 cm/s (…)”
La qual cosa porterebbe ad un ulteriore aumento portata di emissione da pozza pari a circa 3,5 volte quella indicata nell’edizione della norma del 2016.
Questione finalmente chiusa?
Non proprio, diciamo (again).
Se osserviamo l’equazione, notiamo che la portata è proporzionale alla velocità dell’aria che lambisce la pozza (elevata a 0,78, come già visto in precedenza). Per velocità nulle, cioè, l’evaporazione calcolata di una pozza di infiammabili è nulla. Questo trova una sua giustificazione sperimentale poiché i test di evaporazione sono stati effettuati, nel corso degli anni, con tipiche velocità dell’aria esterna, generalmente superiori alla “calma di vento” (=0,5 m/s). Il particolare, tuttavia, è che la velocità di evaporazione di una pozza in assenza di ventilazione non è sperimentalmente nulla.
Proprio no.
Perché questa considerazione è però importante (a parer mio)?
Perché in ambienti chiusi la velocità dell’aria risulta generalmente limitata. Campagne di misure ripetute effettuate con anemometro a sfera calda indicano valori più bassi della calma di vento. Non nulli, ma limitati. In presenza di tali ridotte velocità dell’aria emerge una portata evaporante che la modellazione convettiva dominante all’aperto non contempla: l’evaporazione dovuta a diffusione legata alla differenza di concentrazione.
Molto lenta.
Ma non nulla.
E se, per esempio, l’equazione di Mackay & Matsugu così come modificata dall’EPA restituisse valori di emissioni prossimi a zero quando, invece, l’emissione diffusiva diviene predominante cosa accadrebbe? Ci troveremo nella condizione di dover gestire, nell’ambito della classificazione ATEX, un nuovo “problema”.
Anticipo che recenti studi hanno misurato l’effetto dell’evaporazione per diffusione, in assenza di ventilazione, confermando l’esistenza del “problema”.
E anche di questo, prometto, discuteremo al Workshop ATEX 2024.
—
PS del 21/1/2024: Se proviamo a calcolare il km dell’acqua con la metodologia proposta da Benitez, gli 0,83 cm/s si ottengono con velocità dell’aria di circa 8 m/s. Insomma, non proprio calma di vento… [cfr. Benitez, J. (2022). Principles and Applications of Mass Transfer: The Design of Separation Processes for Chemical and Biochemical Engineering. John Wiley & Sons]
—
[1] Environmental Protection Agency, USA
[2] Mackay, D., & Matsugu, R. S. (1973). Evaporation rates of liquid hydrocarbon spills on land and water. The Canadian Journal of Chemical Engineering, 51(4), 434-439
[3] Crowl, D. A., & Louvar, J. F. (2019). Chemical process safety: fundamentals with applications (IV Edition). Pearson Education


