Molte sono le tecniche disponibili per la valutazione del rischio, e spesso la scelta dello strumento più adatto occupa una fase preliminare fondamentale.
A questo proposito, la norma IEC 31010:2019 definisce la matrice di rischio come:
“(…) un metodo per rappresentare i rischi in funzione delle loro conseguenze e della loro probabilità[1], e per combinare queste caratteristiche al fine di ottenere una valutazione del livello di significatività del rischio”
In altre parole, la matrice di rischio è uno strumento finalizzato principalmente alla valutazione dei rischi già identificati, più che alla loro analisi o individuazione.
Ma come è costruita una matrice?
Sorprende notare come, nonostante la sua diffusione, i dettagli di design di questo strumento vengano talvolta trascurati.
Vogliamo approfondirli un po’?
Proviamoci!
Costruiamo, preliminarmente una matrice di probabilità e danno, di dimensione 4×4 e rappresentiamola nella figura seguente.
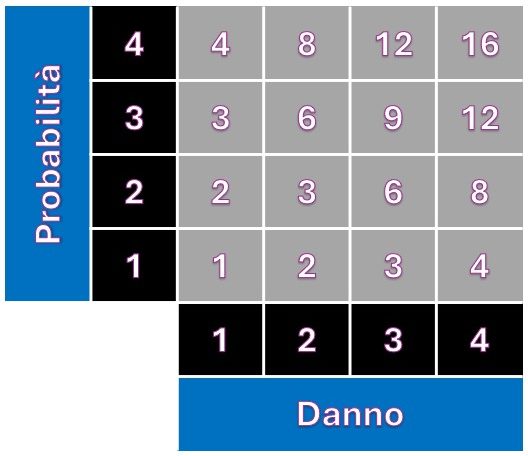
In verticale indichiamo un indice ordinale di probabilità (1 = bassa, 4 = alta) e in orizzontale specifichiamo il danno (1 = basso, 4 = alto).
L’assunzione più comune è che ogni incremento unitario (da “n” a “n+1”) rappresenti un ordine di grandezza, cioè una variazione di un fattore 10.
Ad esempio:
- Danno 1: impatto trascurabile, < 1.000 €
- Danno 2: impatto minore, tra 1.000 e 10.000 €
- Danno 3: impatto rilevante, tra 10.000 e 100.000 €
- Danno 4: impatto grave, > 100.000 €
Dato che il rischio è tradizionalmente definito come:
Rischio = Frequenza × Danno potenziale
una matrice 4×4 porterà a 16 combinazioni possibili, che danno origine a 9 valori numerici distinti (1, 2, 3, 4, 6, 8, 9, 12, 16).
Tutto corretto, no?
No (Vedi citazione)
Una riflessione più attenta mette in dubbio la correttezza dell’approccio moltiplicativo tra indici ordinali, se questi rappresentano ordini di grandezza.
Infatti, la definizione classica di rischio comporta una quantificazione effettiva:
- Danno potenziale: ad esempio in [€/evento] o [giorni di prognosi/evento]
- Frequenza: in [eventi/anno]
E quindi:
Rischio = [€/evento] × [eventi/anno] = [€/anno]
Ma allora, se gli indici che usiamo sono esponenti (base 10), non vanno moltiplicati tra loro, bensì sommati.
Ora, e mi rivolgo al totale dei tre lettori che hanno avuto la pazienza di arrivare fin qui, un conto è dire:
Rischio = f x D = 1000 incidenti/anno x 1000 €/incidente =
= 103 incidenti/anno x 103 €/incidente = 106 €/anno
Altra cosa è concludere che:
Rischio = 3 x 3 = 9
Non ci vuole Eulero per comprendere che gli esponenti non si moltiplicano tra loro ma si sommano.
Il metodo di moltiplicazione degli indici porta ad un sovrastima, rispetto al rischio reale, per alti valori di probabilità e danno mentre, all’opposto, tende a sottostimare il rischio nel caso di valori unitari degli indici.
In questo caso, quindi, un rischio che verrebbe valutato quantitativamente 106, un milione di €/anno, sarebbe stimato uguale a 109, un miliardo di €/anno!
Quindi, ripetiamo insieme:
“Gli esponenti rappresentativi degli ordini di grandezza del rischio non si moltiplicano ma si sommano”
La conclusione alla quale siamo, provvisoriamente, giunti ci conduce quindi a ridisegnare la matrice di rischio nel modo descritto nella figura seguente.
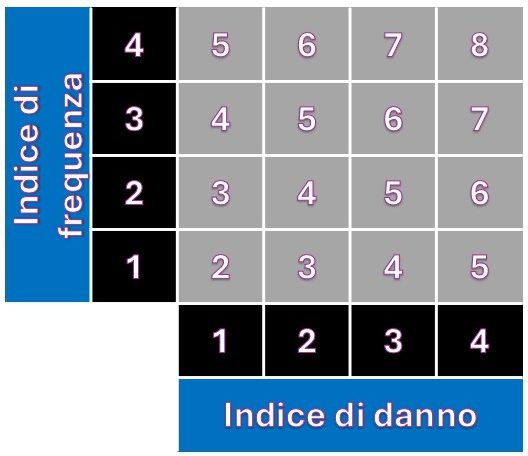
Avendo modificato:
- “Probabilità” con “Indice di frequenza”
- “Danno” con “Indice di danno”
e sostituito il prodotto tra gli indici con la loro somma, assimilandoli ad esponenti rappresentativi delle soggiacenti dimensioni di “danno” e “frequenza“.
Un paio di considerazioni, a valle di questa immagine:
- Le curve di iso-rischio diventano diagonali (dall’alto sinistra verso il basso destra)
- l’estensione della matrice “euleriana”, prima compresa nel rapporto max/min=16/1=16, ora è più compressa: max/min=8/2=4.
Definizione delle zone di rischio nella matrice
Una volta definita la struttura della matrice, si può procedere all’identificazione delle zone di rischio, tenendo conto anche del fenomeno dell’avversione al pericolo[2] e delle indicazioni normative[3].
I gradi di libertà della matrice sono assunti con il seguente criterio:
- Danno potenziale: da 10³ a 10⁶ [€/evento]
- Frequenza: da 10⁻³ a 1 [eventi/anno]
MATRICE IEC FMEA
La prima matrice che sottoponiamo a verifica è quella inclusa nella norma IEC 60812:2018 [Analisi dei modi e degli effetti di guasto (FMEA e FMECA)].
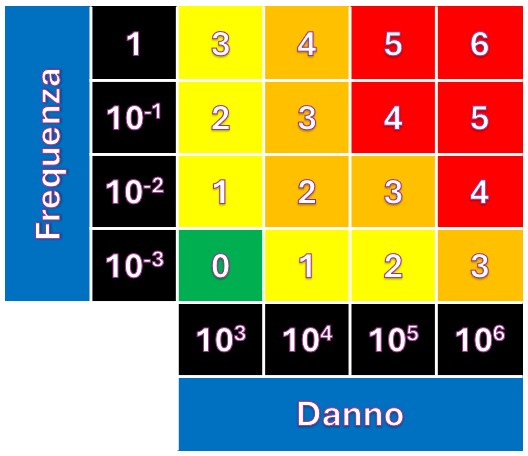
In questa matrice, la parte “rossa” appare fortemente ampliata e, per converso, la parte “verde” è costituita da un solo quadrante. Sono peraltro presenti inconsistenze nella definizione dei progressivi aggravi di rischio in senso diagonale, in particolare in riferimento alla diagonale di iso-rischio pari a 2 [unità di costo/anno].
MATRICE CCPS
Facendo invece riferimento alla classica matrice di valutazione proposta dal CCPS americano nella seguente pubblicazione:
si verifica una situazione sostanzialmente opposta rispetto a quella presentata nell’IEC 60812.
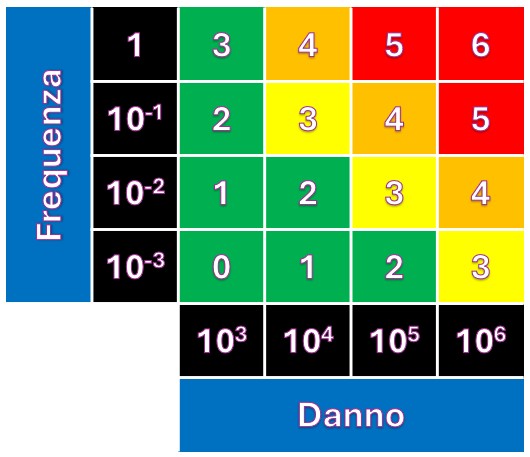
È presente un’ampia zona di rischio accettabile “verde” una limitata presenza della zona ALARP “gialla” e una molto modesta pesatura degli aspetti connessi all’avversione al pericolo. È presente anche un’anomalia minore nella transizione tra rischio accettabile “verde” all’aumentare del danno potenziale: non è previsto il passaggio ALARP: la transizione contempla infatti un passaggio diretto dalla zona “verde” a quella “arancione” in corrispondenza della frequenza di un incidente all’anno.
MATRICE IEC VDR
Forse una miglior opzione, maggiormente rispettosa dei criteri che ci siamo fino ad ora dati, è quella presentata nella norma IEC 31010:2019 [Gestione del rischio. Tecniche di valutazione del rischio].
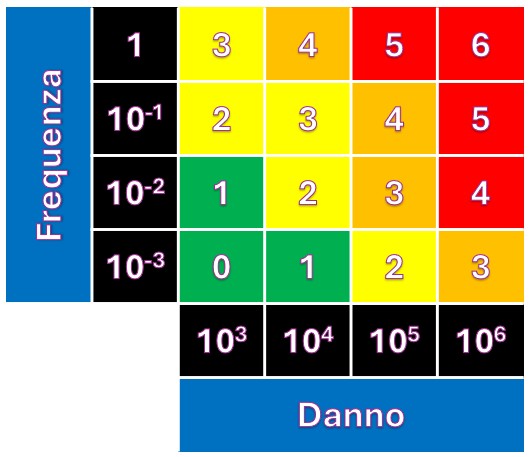
Questa matrice possiede, infatti, una corretta transizione di colore sia in senso orizzontale che verticale. Anche le diagonali di iso-rischio risultano correttamente bilanciate, sia in termini di transizione che di aggravio di rischio che è comunque tenuto in considerazione, senza l’enfasi eccessiva che ne è stata data nella norma IEC 60812:2018.
Conclusione
La costruzione di una matrice di rischio non è banale.
Usare indici ordinali che rappresentano ordini di grandezza comporta errori gravi se si applicano operazioni matematiche non coerenti (come la moltiplicazione di esponenti).
Riconoscere questo aspetto aiuta a costruire matrici più robuste e intrinsecamente coerenti.
– – –
[1] Il termine inglese corretto è “likelihood” che in italiano è tradotto genericamente come “probabilità”. Il problema, però, è che il significato di “likelihood” in inglese è più ampio: è infatti un “contenitore” nel quale è presente la probabilità quantitativa (es. %), la probabilità qualitativa (es. alto, medio, basso) e la frequenza (es. eventi/anno).
[2] L’avversione al pericolo è la tendenza a tollerare meno i rischi caratterizzati da bassa frequenza di accadimento ma conseguenze molto gravi, rispetto a quelli con alta frequenza e danni modesti, anche quando il prodotto frequenza×danno risulta identico
[3] Le proposte presentate sono contestualizzate ed adattate alla dimensione della matrice 4×4
Commento (1)
Euro Ginobili - 13 Ottobre 2025
Buon giorno Marzio, ho letto con estremo interesse quanto hai scritto a proposito delle matrici di rischio, ma per approfondire maggiormente vorrei porti la seguente domanda:
Nel documento si afferma giustamente che, quando le classi di probabilità e di danno rappresentano ordini di grandezza (p.es. 10⁻³…10⁰ e 10³…10⁶), il rischio andrebbe valutato sommando gli esponenti piuttosto che moltiplicando gli indici ordinali.
Vorrei capire se nella tua impostazione gli indici di classe (1, 2, 3, 4, …) sono formalmente associati a valori numerici specifici (es. 1 → 10⁻³, 2 → 10⁻², ecc.) oppure se la scala resta puramente qualitativa e la somma è solo un criterio di ranking.
In altre parole:
hai definito un mapping esplicito fra ogni classe e un valore rappresentativo di frequenza e danno (in unità fisiche o monetarie)?
oppure l’adozione della somma degli indici è intesa solo come metodo di confronto relativo?
Capire questo punto è essenziale per valutare se la matrice può essere considerata quantitativamente coerente con la definizione
𝑅 = 𝑓 × 𝑑 o se resta una matrice semi-quantitativa a ordini di grandezza.