Il mio rapporto con la formula di “Fauske modificata” risale al 1999, anno di nascita della prima edizione dell’ormai ex Guida CEI 31-35.
L’equazione di cui discuto, provvidenziale in molti casi, consente di calcolare la distanza di una dispersione passiva in corrispondenza della quale un rilascio di infiammabile “vede” una data concentrazione (tipicamente l’LFL o un suo sottomultiplo).
La prima edizione della Guida CEI 31-35:1999 riportava, a questo proposito, due versioni dell’espressione matematica: una prima che modellava la relazione di concentrazione di infiammabile in funzione della distanza, per rilasci prossimali al suolo:
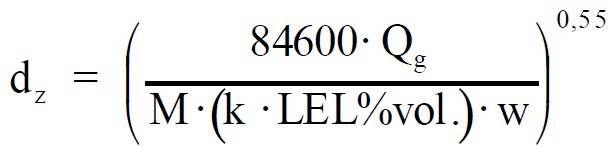
e una seconda volta a stabilire la correlazione tra la distanza pericolosa e la concentrazione per rilasci soprasuolo nei quali la diluizione con l’aria si verificava da tutte le direzioni (in prossimità del suolo, infatti, la diluizione con l’aria non è assicurata e l’estensione si amplia).
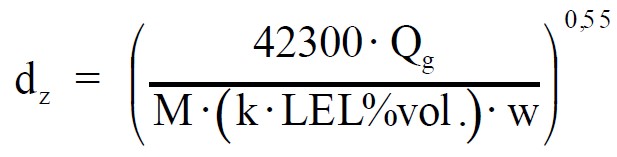
L’evoluzione darwiniana dell’equazione l’ha portata, nella quarta edizione della Guida CEI 31-35:2012, ad essere così rappresentata:
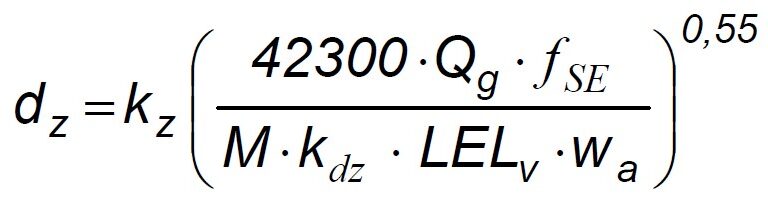
Bruttissima! Infarcita di coefficienti correttivi che snaturavano l’efficacia del modello matematico e annebbiavano il segnale con rumore di fondo.
Si noti tuttavia l’esponente: 0,55. Ci ritorneremo.
Il profilo di concentrazione per emissioni in altezza è dunque sopravvissuto, nel 2012, quello per rilasci prossimali al suolo è invece stato soppresso (senza peraltro essere giustificato).
Perché sto ammorbando i soliti miei tre lettori con questi ragionamenti?
Perché la “fonte” dell’equazione, che fino a quando era in vigore la Guida poteva essere trascurata, ora è necessario identificarla (la Guida CEI 31-35:2012 è stata infatti abrogata nell’ottobre del 2018).
La Guida non rappresenta quindi più lo stato dell’arte sull’argomento ed è ora indispensabile comprendere a pieno l’origine di questa “magica” equazione che così bene simula la dispersione passiva di Pasquill-Gifford nel campo vicino in presenza di rilasci non catastrofici.
Da dove salta fuori, insomma?
Quella che ora vado a raccontare è la “storia” della mia piccola ricerca sull’argomento.
Il primo approccio tentato, volto alla ricerca della fonte prima dell’equazione, è stato diretto: ho consultato la bibliografia delle varie edizioni della Guida 31-35 che nel corso degli anni si sono succedute. L’indicazione era specifica ed inequivoca. Ogni pubblicazione infatti specificava che l’equazione di “Fauske modificata” era stata derivata da un bollettino sulla sicurezza degli impianti chimici che l’Imperial Chemical Industry britannica pubblicava negli anni ’70. Il riferimento era quindi all’ “ICI Safety Bulletin 74/8”. Ai tempi delle prime edizioni della Guida CEI 31-35 questo documento era sostanzialmente introvabile. Successivamente l’IChemE (Institution of Chemical Engineers), sistemando gli archivi, l’ha reso disponibile. E, come è evidente consultando il precedente link, non si parla in alcun modo di equazione di Fauske, tantomeno modificate. Andata “buca” la via principale per l’accesso alla fonte ho cercato di percorrere più tortuose vie secondarie, approfondendo l’opera di Hans K. Fauske scoprendone gli importanti contributi in tema di efflussi bifase e rilasci da valvole di sicurezza. Però, anche in questo caso, nulla che riportasse all’equazione contenuta nella Guida 31-35.
Per un po’ mi rassegnai: non sempre si raggiunge la fonte di quanto si utilizza e, seppur con precauzione, ho continuato ad utilizzare questa straordinaria “macchinetta” numerica.
Poi accadde qualcosa.
Nel mio peregrinare su google scholar mi imbattei in un manuale (del quale francamente non ricordo i riferimenti) che citava una equazione di tal “Katan”, un ingegnere britannico che operò a cavallo degli anni ’50 e ’60.
Ricercai i riferimenti, contattai la British Library (l’unica istituzione che conservava una copia del paper originale) e mi feci inviare il seguente articolo:
• Katan L L. (1951). “The fire hazard of fuelling aircraft in the open”. Fire. Research Technical Paper No 1. HMSO

L’autore, attraverso una sperimentazione specifica finanziata dall’ufficio centrale antincendi inglese, elaborò un’equazione che calcolava il decremento, con la distanza, della concentrazione del rilascio di un infiammabile. In particolare la ricerca era finalizzata ad individuare la distanza pericolosa creata nelle fasi di rifornimento degli aeromobili dell’epoca (effettuate senza alcun recupero dei vapori).
Lì dentro, a pagina 14, faceva capolino questa equazione:
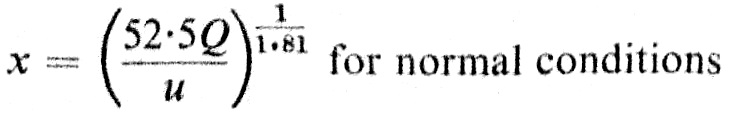
Nell’equazione i termini (portata di rilascio e velocità dell’aria) venivano cioè elevati all’esponente:
“1/1,81”
E 1 diviso 1,81 è esattamente uguale a 0,55.
Il medesimo esponente presente nell’equazione di “Fauske modificata”.
Era una coincidenza oppure era la volta buona?
Purtroppo la velocità dell’aria (u) era espressa in “piedi al secondo” e la portata di emissione (Q) in “galloni al secondo”, ma, secondo me, era molto più di niente.
Avevo (forse) trovato la fonte dell’esponente “0,55”.
Scoprii successivamente che le ricerche di Katan fecero “germinare” tutta una serie di altre relazioni ancorate a quella forma tipica di espressione.
L’opera più autorevole che riprese quell’equazione e la sistematizzò a fini di valutazione del rischio fu la seguente:
• Mecklenburgh, J C. (1985). “Process plant layout”. Halsted Press.
Nel manuale si riprendevano, citandoli, gli studi di Katan e a pagina 531 veniva presentata la seguente espressione:
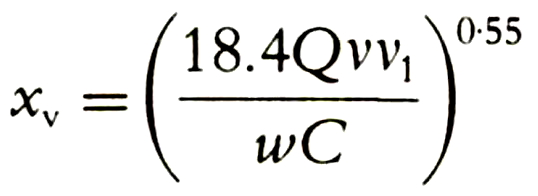
Non badate ad alcuni termini che possono confondere: c’è anche qui la portata (Q), la velocità dell’aria (w) e, rispetto all’equazione di Katan, esiste pure la concentrazione (C).
Vogliamo ora provare a “ripulire”, “disidratare” dai termini confondenti e “uniformare” l’equazione di “Katan-Mecklenburgh” (KM) e quella di “Fauske modificata” (FM) presente nell’ultima edizione della CEI 31-35?
Dai, “famolo” (cit.)!
Utilizzeremo, per questo, la simbologia presente nell’ultimo grido della scienza e della tecnica sull’argomento ovvero la Norma EN IEC 60079-10-1:2021.
L’equazione di Fauske modificata (FM) diventa la seguente:
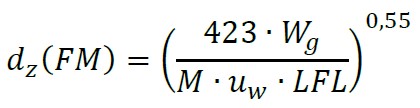
Dove:
– dz è la distanza pericolosa [m]
– Wg è la portata di rilascio [kg/s]
– M è la massa molare della sostanza [kg/kmol]
– uw è la velocità dell’aria rappresentativa [m/s]
– LFL è il limite inferiore di infiammabilità [vol/vol]
Mentre l’equazione di Katan-Mecklenburg (KM) è di seguito riportata:
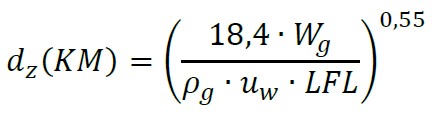
Dove:
– ρg è la densità dei vapori [kg/m3]
Come si vede le equazioni sono simili.
Non uguali.
Simili.
A meno che non si voglia provare a “sostituire il sostituibile”.
Proviamo a rimpiazzare la densità del vapore nell’equazione KM partendo da qui:
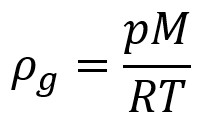
Si ha:
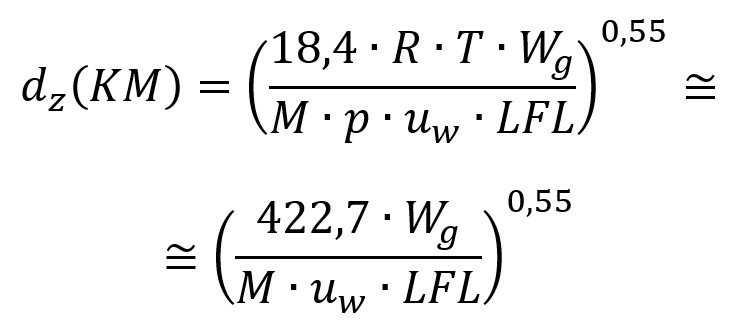
Avendo assunto una T = 280 K (circa 7°C, poco sotto al valor medio atmosferico in UK) e p = 101325 Pa, la pressione convenzionalmente assunta come atmosferica.
Alla fine di tutto questo peregrinare cosa abbiamo scoperto?
Abbiamo scoperto che l’equazione di Fauske modificata della ex Guida CEI 31-35 non è null’altro che l’equazione di Katan-Mecklenburgh!
Non trovate sia ben più di “fico”?
Per essere più chiari:
![]()
Forse non esiste più la bibliografia e la fonte dell’equazione FM ma certamente si può fare affidamento a tutto il materiale prodotto, nel corso degli anni, per l’equazione KM.
CONCLUSIONI
Almeno tre.
La prima: la bibliografia allegata ad un documento è di importanza straordinaria. Se vogliamo inserirla deve essere precisa altrimenti “mandiamo” a spasso i “nerd” per decenni.
La seconda: probabilmente l’equazione che l’ex Guida CEI 31-35 ha denominato di “Fauske modificata” non c’entra nulla con Fauske. L’unico legame che probabilmente esiste con quello straordinario scienziato è la “k” nel cognome, che tuttavia è quella di Katan.
La terza: l’equazione KM può lavorare anche in condizioni non atmosferiche. Tale aspetto risulta invece precluso utilizzando l’equazione di “Fauske modificata”.
Ah, si: una quarta. I fili di Arianna possono, a volte, presentarsi sotto forma di esponenti numerici.
—
Vediamo quanti sono giunti alla fine di questo post?
Solo uno?
Pensavo peggio… 😊

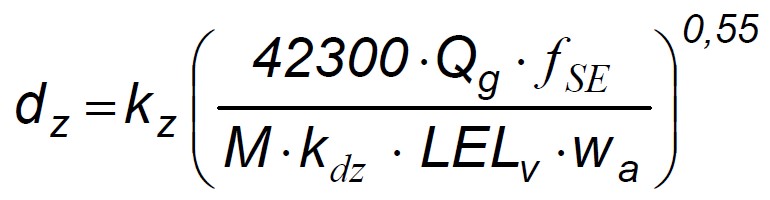
Commenti (11)
Euro Ginobili - 30 Agosto 2022
Interessante opera di investigazione! Complimenti e grazie per la condivisione.
Mario T - 30 Agosto 2022
Interessantissima ricerca bibliografica!
Zerella Luigi - 30 Agosto 2022
Marzio è veramente in gamba. A me quella formula è sempre piaciuta e quando potuto utilizzata anche all’indomani dell’abrogazione.
Andrea Baraldi - 31 Agosto 2022
Grazie davvero per la ricerca e per l’opera di divulgazione in questo argomento complesso… almeno per me.
Giorgio Leuratti - 13 Aprile 2023
Caspita, che ricerca affascinante, complimenti!
Rimane però il fatto che se uso la prima formula in alto (quella della 31-35 con il 42300), al netto dei coefficienti kz, kdz ed f (posti = 1), trovo un valore di dz di 2 ordini di grandezza maggiore di quello calcolato con la formula in basso, quella con il 422,7 (il che è normale visto che, non considerando i coefficienti di sicurezza/correttivi, e dato che tutti gli altri termini delle 2 formule sono uguali, il rapporto tra i 2 risultati è proprio 42300/422,7…). Domandona: le 2 formule finali dz(KM) e dz(FM) in che modo possono essere utilizzate?
Marzio Marigo - 13 Aprile 2023
In realtà le due equazioni restituiscono il medesimo risultato. Nell’equazione FM l’LFL si inserisce in % (Es. LFL = 2%, inserisci 2) mentre nella KM l’LFL vale nella sua forma “nativa”, e quindi 0,02.
Risposto alla prima, vengo alla seconda: le equazioni si utilizzano per rilasci passivi di gas infiammabili. Emissioni, cioè, prive di quantità di moto che vengono disperse, nel campo vicino, dall’azione locale del vento. Tipico è il caso delle valvole di respirazione di serbatoi oppure le emissioni passive derivanti dall’evaporazione di pozze incluse in cordoli.
Saluti
MM
Giorgio Leuratti - 14 Aprile 2023
Grazie mille!
Potrebbero quindi essere utilizzate anche nel caso di un rilascio di idrogeno dovuto a perdite strutturali da una connessione di alimentazione di un gascromatografo, in un ambiente chiuso scarsamente ventilato (dove peraltro il valore di Qc è così basso da essere al di fuori dell’area dei grafici della norma)?
Buona giornata
Giorgio
Marzio Marigo - 14 Aprile 2023
Il linea di massima quell’equazione si applica nel caso di rilasci non sonici, quindi in presenza di pressioni (assolute) di emissione inferiori a, circa, 1,7-1,9 bar.
Poi c’è da capire se il rilascio sia, o meno, ad alta diluzione, ma qui si entra in EN IEC 60079-10-1:2021.
Ed altre cosine ancora.
Saluti
MM
Fabio Emanuele - 22 Luglio 2023
Interessantissima investigazione!
luigi - 5 Novembre 2023
Interessantissimo.
A questo punto il dubbio “butto via la guida CEI 31-35” è sempre più difficile da risolvere!
Alborghetti Enzo - 14 Agosto 2025
Una sola parola: GRAZIE